Distance Metrics - How to Calculate the Distance Between Multiple Locations
geospatial
map
distance
Introduction
Have you ever wondered how apps like Google Maps find the fastest route to your destination? Or how delivery companies optimize their routes to save time and fuel? The secret lies in distance metrics—mathematical methods used to measure how far apart two or more locations are. Measuring distance isn’t just about drawing a straight line between two points. Depending on the situation, different methods are used. A straight-line measurement works fine for short distances, but when dealing with road networks, city layouts, or even the Earth's curvature, more sophisticated approaches are needed. Whether you're mapping out the best delivery routes, analyzing customer distribution, or simply planning a road trip, understanding how to calculate the distance between locations is essential. There are several ways to measure distance, and each method serves a different purpose depending on the use case. Let’s dive into the most common distance metrics and see how they work in real-world scenarios.
Theory
In this guide, we’ll explore various distance metrics, from simple Euclidean distance (straight-line measurement) to more advanced methods like Haversine distance (for calculating global distances) and road network distance (for real-world travel).
- Euclidean Distance: The Straight-Line Approach Euclidean distance is the simplest way to measure the gap between two points. It’s the “as-the-crow-flies” distance—the shortest path between two locations on a flat surface.
- Manhattan Distance: Moving in a Grid Named after the grid-like layout of New York City streets, Manhattan distance (or “taxicab distance”) measures distance by only allowing movement in horizontal and vertical directions.
- Haversine Distance: The True Globe Measurement Euclidean and Manhattan distances assume a flat world—but the Earth is a sphere! For longer distances, we need a formula that accounts for the planet’s curvature. That’s where Haversine distance comes in. We will be working with longitude-latitude, which represents the earth’s spherical surface — as opposed to the standard plain 2D coordinates system in (x,y). Because of this, the Euclidean distance is not the best distance metric to use here. Instead, we will use the Haversine distance, which is an appropriate distance metric on a spherical surface.
- Vincenty Distance: Similar to Haversine but More Accurate While Haversine is great for quick estimates, Great-Circle Distance (also called “Vincenty’s formula”) provides even greater precision by accounting for the Earth’s ellipsoid shape rather than assuming it’s a perfect sphere.
- Road Network Distance: The Real Travel Distance In most cases, people and vehicles don’t move in straight lines—they follow roads, highways, and pathways. This is where road network distance comes in. Uses Geographic Information Systems (GIS) or mapping APIs to calculate real-world travel distances. there are:
- Open Source Routing Machine (OSRM) - is an open-source routing engine and accompanying set of libraries for use with OpenStreetMap data.
- Valhalla - is an open-source routing engine and accompanying set of libraries for use with OpenStreetMap data.
- Google API
Which Distance Metric Should You Use?
| Metric | Best For | Example Use Case |
|---|---|---|
| Euclidean | Straight-line distance | Finding the closest supplier |
| Manhattan | Grid-based movement | Estimating city travel distances |
| Haversine | Globe-based distances | Calculating flight paths |
| Great-Circle | High-accuracy geospatial calculations | Aviation, shipping routes |
| Road Network | Real-world travel distance | Ride-sharing, delivery logistics |
Dataset
Load dataset
we generated 5 random data to create longitude and altitude data.
dist = [[ 1.616204 , 99.289473 ],
[ 1.450185 , 99.309193 ],
[ 1.646177 , 99.264188 ],
[ 1.37482 , 99.302575 ],
[ 1.707857 , 98.824418 ],]
Points
| 0 | 1 | |
|---|---|---|
| 0 | 1.6162 | 99.2895 |
| 1 | 1.45019 | 99.3092 |
| 2 | 1.64618 | 99.2642 |
| 3 | 1.37482 | 99.3026 |
| 4 | 1.70786 | 98.8244 |
The Code
By calling optimization.compute_distances, distances are calculated based on the specified distance calculation type. This function returns distance (in meters) and duration (in seconds) as a DataFrame.
distance,duration = optimization.compute_distances(dist,types='osrm')
This function requires the following parameters:
- dist (
geodataframe): Data location and value - types (
string): distance type calculator
in types parameter, we can calculate with there values:
- euclidean
- haversine
- vincenty
- osrm
- osrm_path
- other values for non-geospatial distance
The result
Distance
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 29.1142 | 10.0799 | 40.5882 | 93.2065 |
| 1 | 29.1142 | 0 | 36.0844 | 11.474 | 91.7407 |
| 2 | 10.0799 | 36.0844 | 0 | 47.5441 | 100.162 |
| 3 | 40.5882 | 11.474 | 47.5441 | 0 | 85.8765 |
| 4 | 93.2065 | 91.7407 | 100.162 | 85.8765 | 0 |
Duration
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| 0 | 0 | 1281.5 | 1193.2 | 1931 | 4576.4 |
| 1 | 1281.5 | 0 | 2282 | 649.5 | 3893.8 |
| 2 | 1193.2 | 2282 | 0 | 2925.8 | 5571.2 |
| 3 | 1931 | 649.5 | 2925.8 | 0 | 3827.2 |
| 4 | 4576.4 | 3893.8 | 5571.2 | 3827.2 | 0 |
Route path
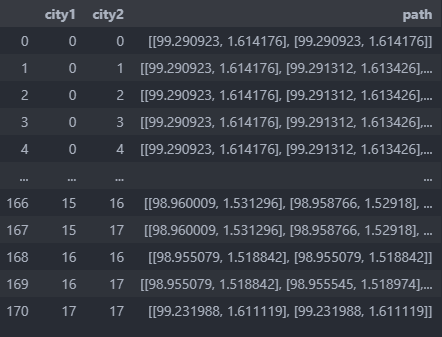
use case
TSP and VRP case

Final Thoughts
Choosing the right distance metric depends on the scenario. If you’re working with local routes, Manhattan or road network distance might be best. For global logistics, Haversine or Great-Circle Distance provides better accuracy. Understanding these metrics helps businesses optimize delivery routes, reduce costs, and improve customer experience.