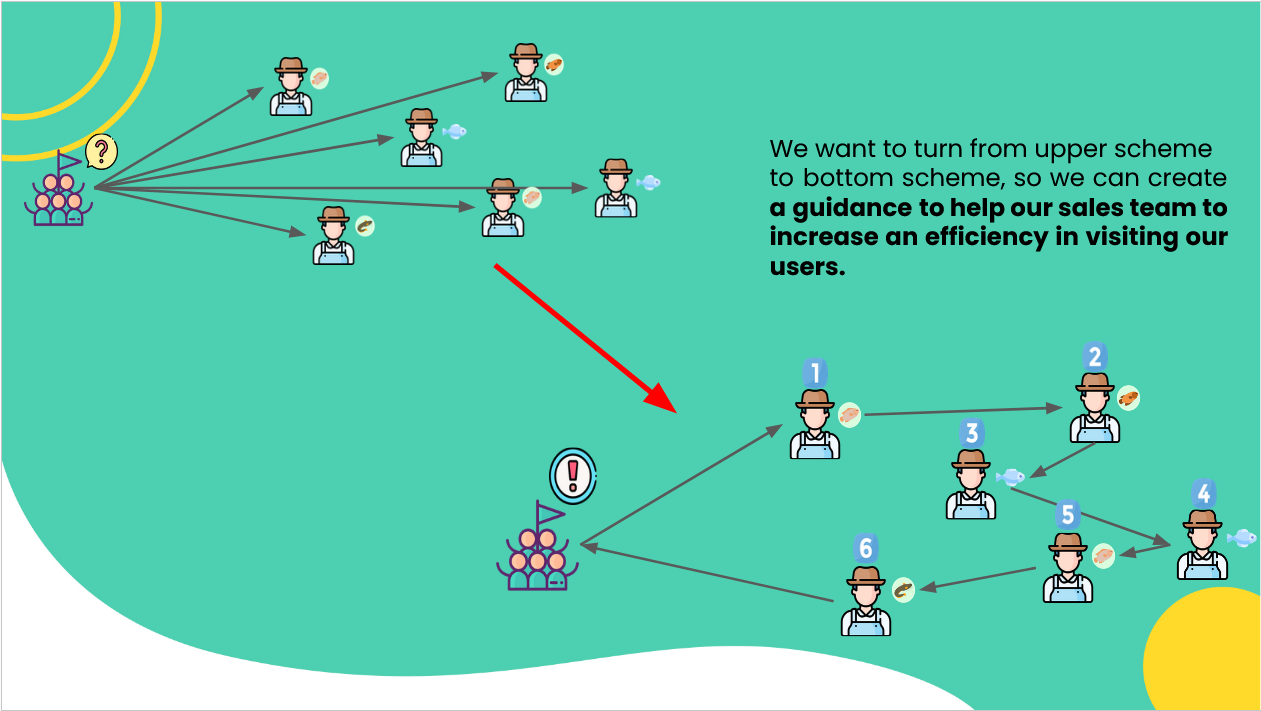
Route-based combinatorial optimization problems

geospatial

map

Optimization

Introduction

Route-based combinatorial optimization problems set out to solve the most efficient route from point A to a set of destination points.

These problems can be simple, where a person or a vehicle departs a starting point and must travel to a set of destination points while visiting each point only once before returning to the origin point, all while minimizing the distance traveled. This is formally known as the Traveling Salesperson Problem (TSP). In another words, Travelling salesman problem (TSP) Try to solve this question:

Given a set of cities and the distances between each pair of cities, what is the shortest possible tour that visits each city exactly once, and returns to the starting city?

This problem can easily become more complicated when you add in a set of vehicles or people visiting destinations instead of a single vehicle or person in the TSP problem. This is known as a Vehicle Routing Problem (VRP). To solve this problem, you must find the optimal routes for a set of vehicles to traverse to visit a given set of customers. Additional complexity can be added to this problem class in instances where the vehicles have a set capacity that can be loaded into them. This is known as a Capacitated Vehicle Routing Problem (CVRP).

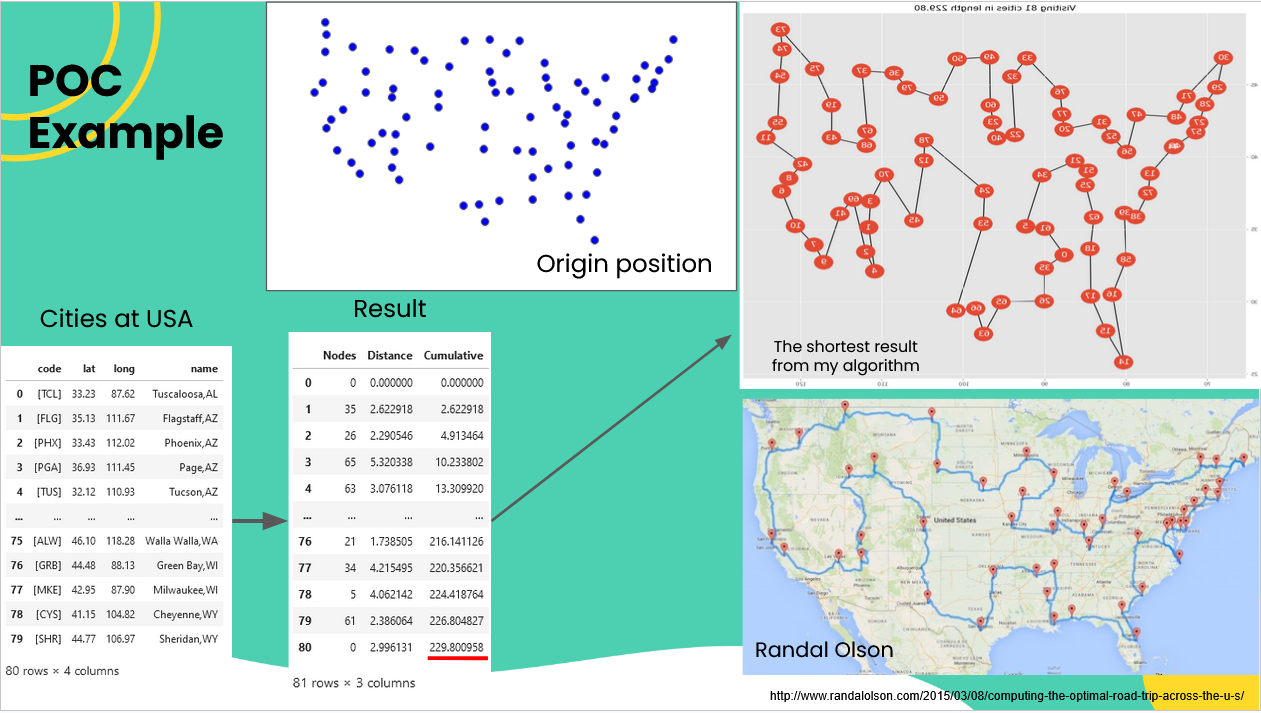
POC Example

In this example we use cities of USA, you can find their location and plot below.

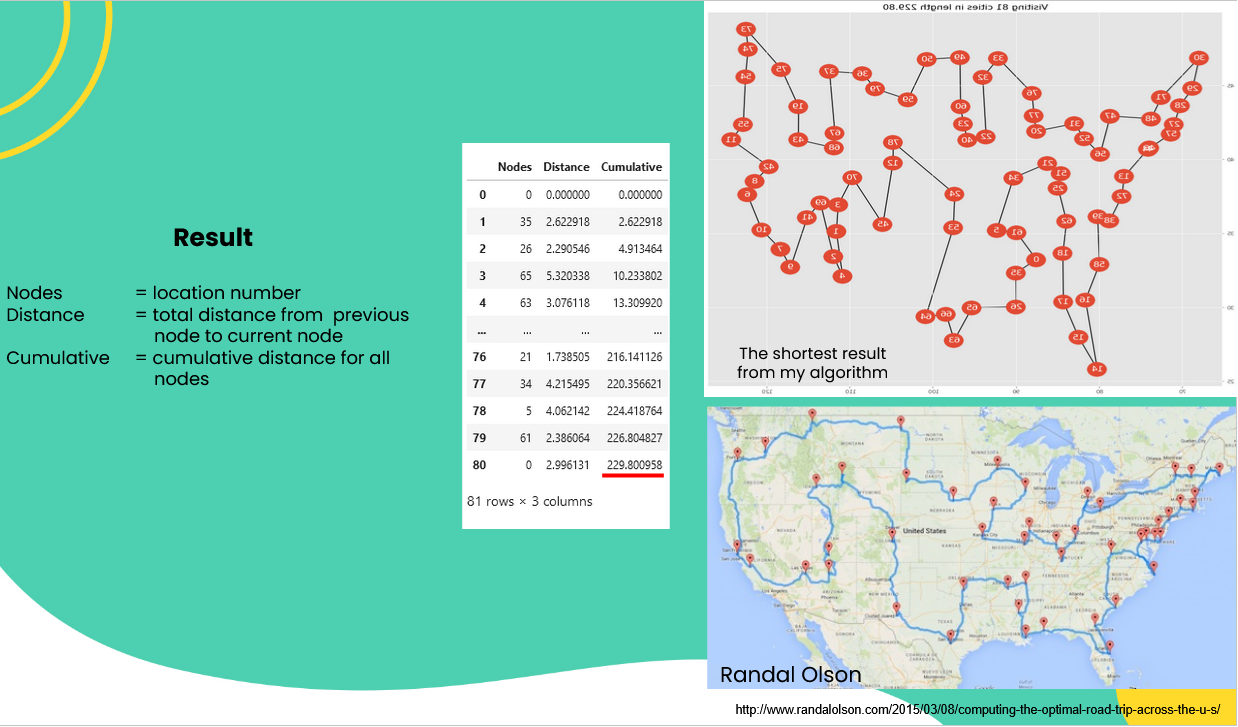
On this result, we use Euclidean distance to make calculation faster. After we applied TSP to our dataset, we can found the shortest route was 229,8. You can find the result in number at table below or in plot result on the right. As comparison, we provide another result from randal olson.

Schema

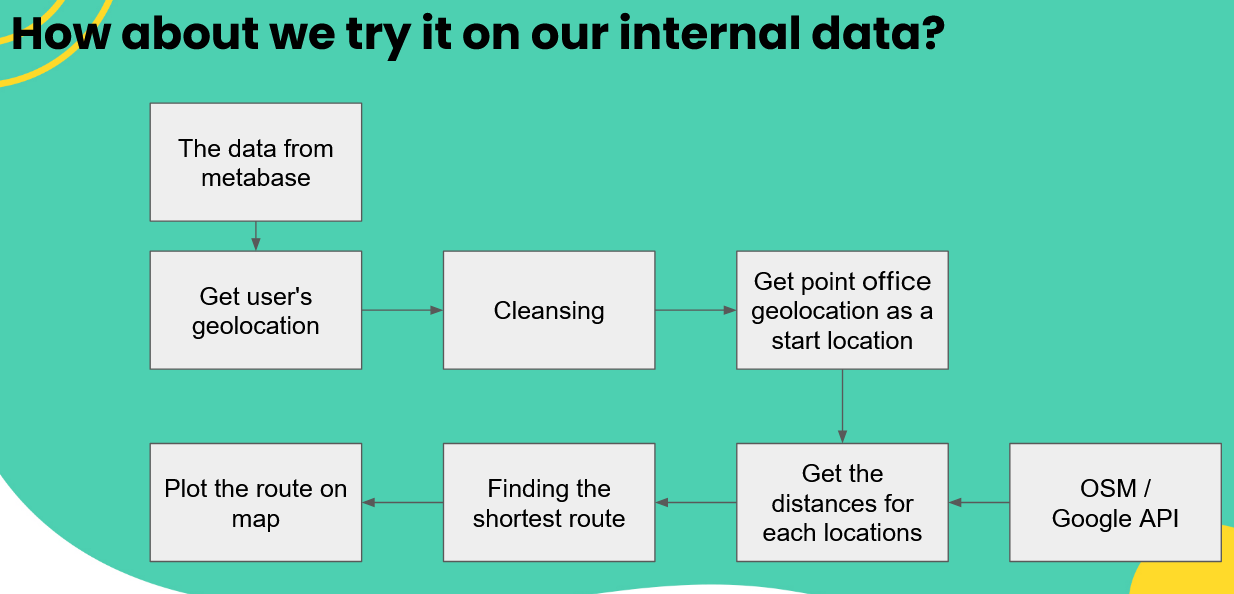
Get the distances for each locations

There are several method to get the distances for each locations. I.e.:

• Openstreetmap.org (OSM) is a digital map database of the world built through crowdsourced volunteered geographic information (VGI). it is means free but not accurate. You can read usage policy OSM here.

• Google Maps Platform is a web mapping platform and consumer application offered by Google. We need billing to access their API. It is means reliable but costly.

For this project we use OSM to proving our method. we can use combination of distance and other values as long as the goal is align with TSP which is to minimization value (to be specific for TSP is minimization distance value).

For this project we can use OSM path method, for example to see how good our result is. We use OSM path API (http://project-osrm.org/docs/v5.10.0/api/) to get short distance and best route between 2 locations.

advantage:

• Free to use

disadvantage:

• OSM path is not as accurate as Google API so the result may be slightly difference comparing with google map or actual distance and route.
• Sometimes the API a little bit lagging so the result maybe not as fast as google API.
• Some areas or locations can’t be found on OSM path, and it will return as Null value.

But again, this is a trade-off between accuracy and cost. But with the expansion of the OSM community and usage, these issues about accuracy will be gradually better.

Finding the shortest route

There are several methods that we can use to find the shortest route in TSP. Although All of them can’t to be the best method due to TSP is NP-hard, but we can use approximation method such as:

• OR optimization
• Genetic algorithm

Both of them have advantages and disadvantages. Because these methods were approximation, there is no guarantee that the resulting model is the best model.

The input of this model is distance matrix that contain distances from and to every locations.

Example with our data

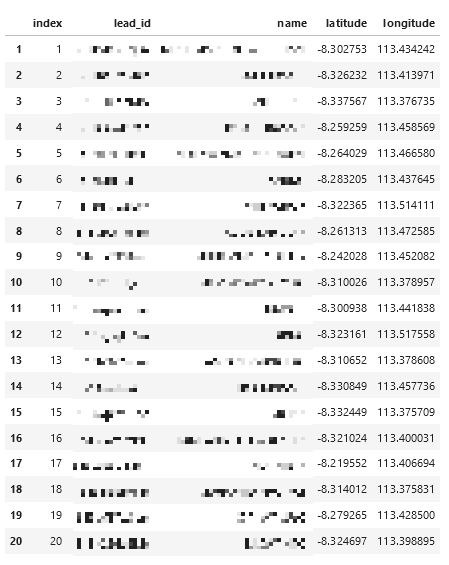
For this example we take the data at jember point.

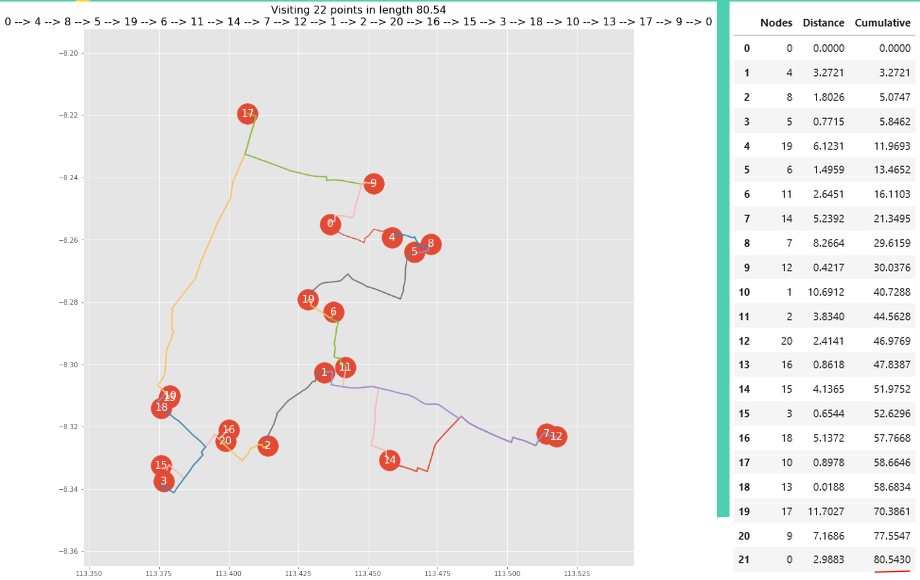
The Result

In this result we use OSM as distance measurement and OR optimization to calculate shortest distance. We found that if we start from jember point office at 0, we can go to user 4, user 8 and so on, to get shortest distance (80.54 km) to visit all user in jember area and back to jember point again. The route start from 0,4,8, and so on, where number base on index column from previous slide.

Find more interactive map in HTML here link

Number in this map base on suggest visiting order i.e. from jember point at blue marker, we go to 2,3,4, and so on. There is user information (using tooltip) if you open HTML file above.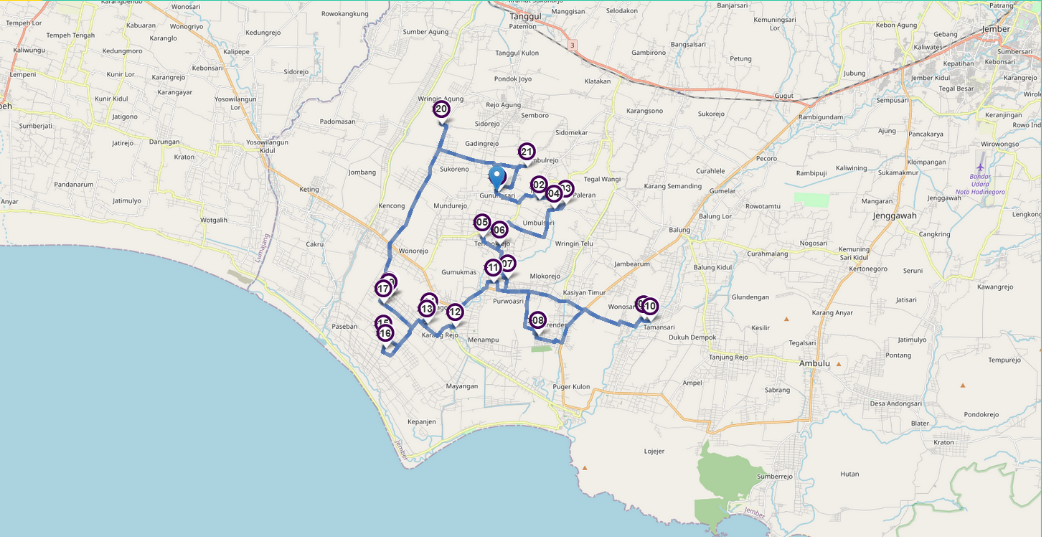

Expand the model from TSP to VRP

If we have this kind question:

Given a set of locations and the distances between each pair of locations, what is the shortest possible tour that visits each location exactly once, and returns to the starting location?

Two of the solutions are: Travelling salesman problem (TSP) or vehicle routing problem (VRP).

In TSP, the goal is to find the shortest route for a person who needs to visit customers at different locations and return to the starting point. A more general version of the TSP is the VRP, in which there are multiple vehicles.

In vehicle routing problem (VRP), the goal is to find optimal routes for multiple vehicles visiting a set of locations. (When there’s only one vehicle, it reduces to the TSP).

From VRP we can add other parameters, such as:

• Capacity constraints, in which vehicles have maximum capacities for the items they can carry.
• Time windows, where the vehicles must visit the locations in specified time intervals, etc.

Constructing a model for VRP

By definition, the goal for VRP is to find optimal routes for multiple vehicles visiting a set of locations.

But what do we mean by “optimal routes” for a VRP?

One answer is the routes with the least total distance. However, if there are no other constraints (such as: capacity, time windows etc) , the optimal solution is to assign just one vehicle to visit all locations, and find the shortest route for that vehicle. This is essentially the same problem as the TSP.

A better way to define optimal routes is to minimize the length of the longest single route among all vehicles. This is the right definition if the goal is to complete all deliveries as soon as possible.

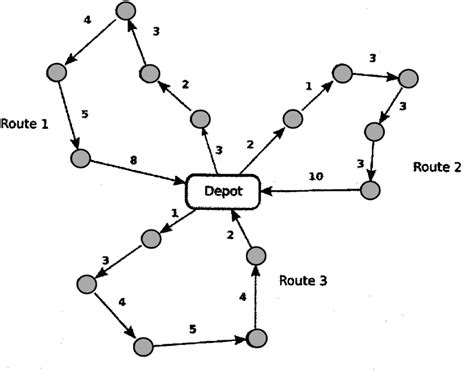
Result VRP

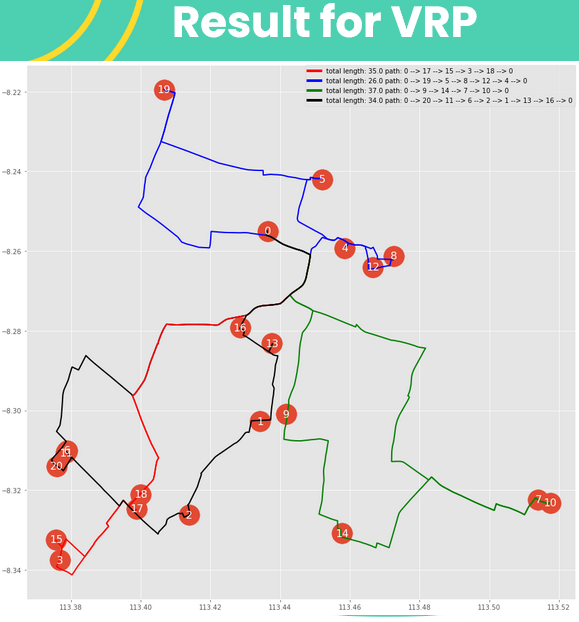
In this part, we use the same data and we apply VRP to get shortest path for 4 vehicles, and we want to make it as equal path as possible. With the numbers as customer’s location and the path colour as shortest path for 4 vehicles, we got the result as the left image:

As you can see at left image, the result of 4 paths are:

• 0, 17, 15, 3, 18, 0 with 35 km length(red line)
• 0, 19, 5, 8, 12, 4, 0 with 26 km length (blue line)
• 0, 9, 14, 7, 10, 0 with 37 km (green line)
• 0, 20, 11, 6, 2, 1, 13, 16, 0 with 34 km (black line)

Although, the second path has shortest path between them, the other path have almost equal length. This will occur because the total distance between the customer’s location can’t be divide by number of vehicle, so there will be a shortest path between them and not fully equal distance.

Find more interactive map in HTML here link

Number in this map base on number at previous slide. We distinct each colours for each vehicles, we we can see clearly every path that each vehicle should take, with blue point as start point or jember point

There is user information (using tooltip) if you open HTML file above.

This result can be improve with several boundary such as:

• Time boundary or time windows - where the vehicles must visit the locations in specified time intervals.
• Minimum point to be visited - where the vehicles aren’t required to visit all locations, but must pay a penalty for each visit that is dropped.
• Capacity constraints - in which vehicles have maximum capacities for the items they can carry.
• Minimum Coverage area
• etc

Some challenges to implement this method

• Completeness of the data and how to collect them
• TSP is NP-Hard*
  • There are several models to solve this problem (all of them fail to become the best solution so far)
  • Trade-off between shortest path and time complexity
• Is it like trying to herd cats? - (if we want to implement this, is there any impact to our business?)

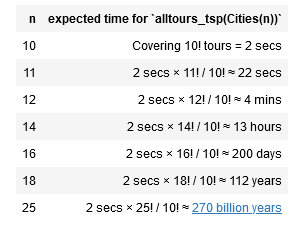
what is TSP is NP-Hard*?

The simplest method to solve TSP problem (so far) is Permutation. All the paths are permutations of the set of all points / cities. The total time required for n cities should be roughly proportional to n!. This means that the time grows rapidly with the number of cities. Really rapidly!

But we can use approximation methods to get shorter computation time with slightly low in accuracy.

Some solutions for these problems

• Completeness of the data and how to collect them
  • Collect location data right now (i.e. by GPS apps, Implement GPS measurement on sales team apps).
  • make location data as mandatory field in the registration form.
• TSP is NP-Hard
  • Use approximation methods to overcome this issue.
  • Breakdown the big chunk problem into few simpler problems. (I.e. create a smaller visiting area to get higher efficiency from our model)
• Is it like trying to herd cats?
  • Is field team really need this guidance to visiting our users?
  • Will sales team use this guidance clearly? Why this matter? Because it is important to measuring how much improvement that we will make with this method.